
가설검정의 4 단계 : 가설 수립 - 실험 설계 - 자료 수집 - 추론결론 도출
ex. 미술관 관람 고객 200명 중 입장권을 온라인 구매한 사람이 150명, 현장구매는 50명이다. 온라인 입장권 구매 고객 중 40명이 미술관 해설 패키지표를 구매하였고, 현장 입장권 구매 고객 50명 중 20명이 미술관 해설 패키지 표를 구매하였다. 미술관 입장권의 온라인/현장 구매여부와 미술관 해설 패키지표 구매여부는 서로 독립인지 검정하시오.
| 가설 수립 | 실험 설계 | 자료 수집 | 추론결론 도출 |
| 미술관 입장권의 온라인/현장구매여부와 미술관 해설 패키지표 사이의 구매여부는 독립적이다 | 온라인과 현장구매 구조와 미술관 해설 패키지표 부분에 대해 기본 조건을 찾고 가설을 설정한다 | 온라인과 현장 구매에 따른 고객의 수 분석, 미술관 해설 패키지표 구매 고객의 데이터 수집 | 귀무가설과 대립가설 도출하고 이를 검정하여 결론 도출 |
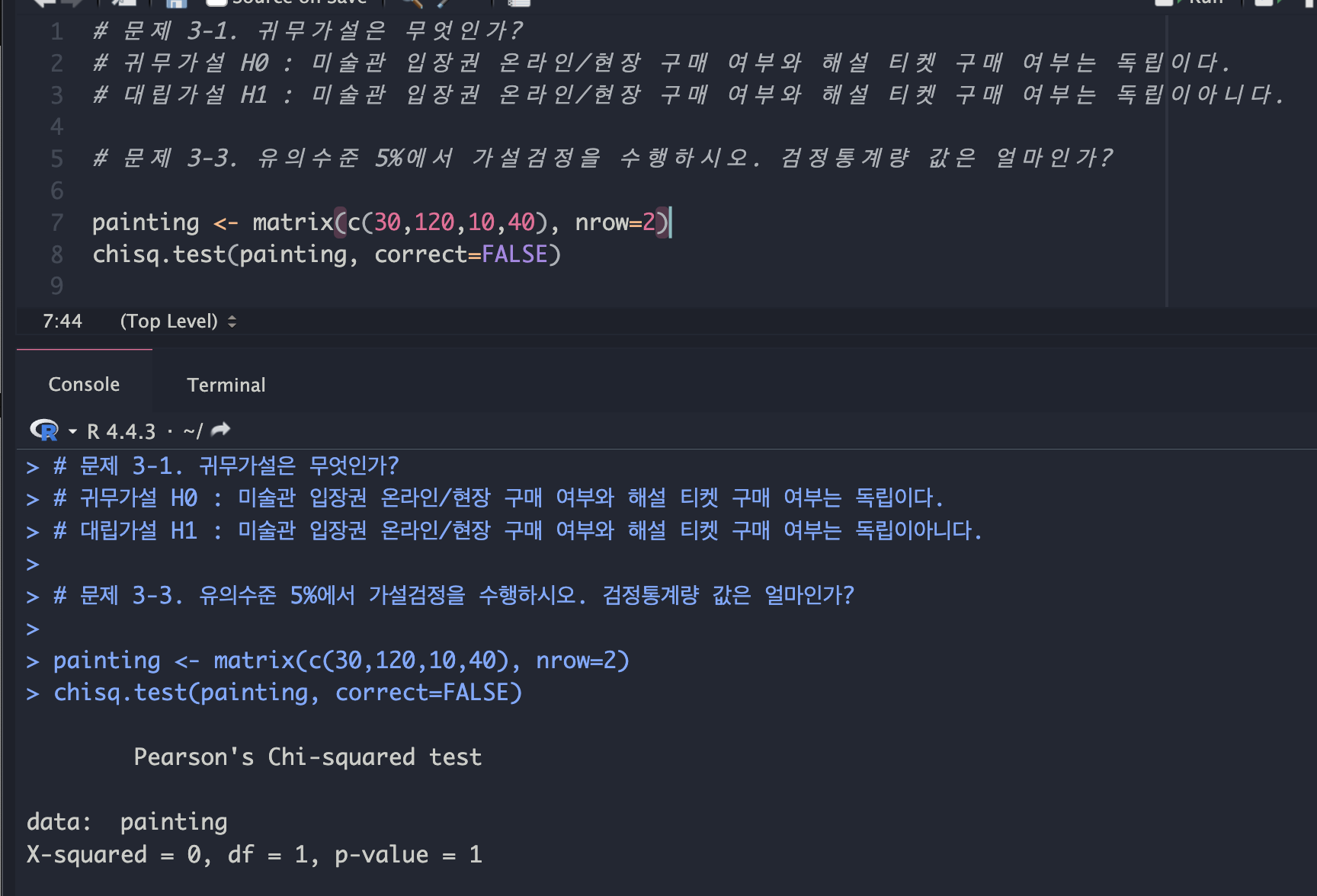
독립성 검정 시행시(연속성 보정은 하지 않는것으로 간주하여 False) 귀무가설과 대립가설을 설정하고, 온라인과 현장으로 구분되는 데이터셋에 대한 집단을 나눈 뒤 painting이라는 변수를 통해 값을 담고(온라인 구매 고객 중 해설 표를 구매한 30명, 구매하지 않은 120명 / 현장 구매 고객 중 해설 표를 구매한 10명과 구매하지 않은 40명) 유의수준 5%을 기준으로 독립성 검정을 시행. 이때 검정통계량 값이 1이며 유의수준 5%일때 p-value가 1 > 0.05 이므로 이 값은 귀무가설을 기각할 수 없으므로 대립가설의 주장은 무의미(독립이 아니다)함. 그러므로 귀무가설에 따라 구매 여부는 독립이다라는 결론을 내릴 수 있음
두 그룹으로 나누어 검정하는 AB 검정 : 처리군, 대조군, 검정통계랑
| 처리군 | 대조군 | 검정통계량 |
| 어떤 조건에 대해 그 조건이 적용된 집단 | 처리군과 대조되는 그 조건이 적용되지 않은 대상집단 | 실험에 따라 처리 효과를 유의미하게 측정하고 분석해서 나타낼 수 있는 객관적 지표 |
가설검정 : 유의성검정이라고도 하며 전통적인 통계적 분석 방법. 귀무가설, 대립가설, 일원검정, 이원검정
| 귀무가설 | 대립가설 | 일원검정 | 이원검정 |
| 기존의 가설. 증명받는 대상의 가설. 우연에 기반한 가정 | 귀무가설과 반대되는 내용의 증명하고자 하는 가설 | 한 방향으로만 일어날 확률을 계산하는 검정 | 양방향으로 일어날 확률을 계산하는 검정 |
통계적 유의성과 p값 : 제 1종 오류, 제 2종 오류, P값이 있으며 우연성에 의해 일어날 수 있는 변동성 외에 결과가 존재한다면 통계적으로 유의하다라고 말할 수 있는 가능성을 일컫음
| 제 1종 오류 | 제 2종 오류 | p-value |
| 우연으로 인한 결과를 실제 효과라고 잘못된 결론 내리는 것 | 실제 효과를 우연에 의한 결과라고 결론 내리는 것 | 귀무가설의 구체화 할 수 있을때 관측된 결과나 이와 같이 특이하거나 극단적 결과를 얻을 확률 |
T 분포와 다중검정, 과대적합, 자유도, 분산분석, F 통계량, 이원분산분석, 카이제곱검정
T 분포 : 수집된 데이터의 횟수 또는 측정값을 포함하는지 표본의 규모가 얼마나 큰지, 측정 대상이 무엇인지에 따라 유의성 검정하는 방법 중 하나이며 스튜던트 분포라고도 함. T 검정에서 관측된 T 통계량을 비교할 수 있는 기준 분포를 의미
다중검정 : 단일 가설검정과 다르게 보다 통계적 유의성 기준을 엄격히하고 유의수준을 세분화하여 보다 더 정확한 결과를 얻는것
과대적합 : 데이터를 가지고 통계적 유의성을 가리는 중에 잡음까지 피팅되는 경우
자유도 : 표본 속 데이터에서 계산된 통계량에 적용된 변화가능한 값의 개수. 표준편차 계산시 분모에서 n-1이며 확률분포에서 자유도 모수에 따라 분포의 모양이 달라짐
ex. 10개의 값으로 이뤄진 표본에서 평균값을 알고 있을 경우 9개의 자유도가 있으며 10번째 값은 9개를 알고 있다면 계산할 수 있기에 자유롭게 변경할 수 없음.
분산분석 : a/b 검정 외 c,d등 여러 그룹간의 차이를 통계적으로 검정하는 절차
F통계량 : 그룹 평균간 차이가 랜덤 모델에서 예상되는 것에서 벗어나는 정도를 측정하는 통게량
이원분산분석 : 여러 그룹의 실험 결과를 분석하기 위한 통계적 절차이며 ab 검정과 비슷한 절차의 확장 ㅐㄱ념으로 그룹 간 편차가 우연에 의해 발생할 수 있는 범위 내에 있는지를 알아보기 위해 사용.
카이제곱검정 : 횟수 관련 검정에 사용되며 예상되는 분포에 맞는 정도를 검정하는 방법. 변수 간 독립성에 대한 기존의 귀무가설이 타당한지를 평가할때 사용
'통계데이터과학과 및 컴퓨터과학 독서' 카테고리의 다른 글
| 4-3. 회귀와 예측 (0) | 2025.04.21 |
|---|---|
| 04-1. 회귀와 예측 (0) | 2025.04.07 |
| 01-2.탐색적 분석 (0) | 2025.03.17 |
| 01-1. 탐색적 분석 (0) | 2025.03.16 |
| 8-3. 그 외 AWS 서비스 3 (0) | 2024.11.25 |